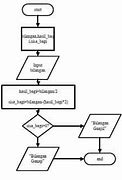
cara menyelesaikan algoritma matematika
See full PDFdownloadDownload PDF
See full PDFdownloadDownload PDF
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
PELUANG menjadi salah satu materi yang muncul di Ujian Nasional SMA dan Ujian Tulis Berbasis Komputer (UTBK). Dalam pelajaran matematika, peluang adalah kemungkinan dari suatu kejadian yang dapat diperoleh dengan perhitungan atau percobaan.
Peluang dapat kita aplikasikan dalam kehidupan sehari-hari. Peluang dapat digunakan untuk mengambil keputusan yang tepat, memperkirakan hal yang akan terjadi, dan mengurangi kemungkinan untuk rugi dalam suatu hal. Peluang juga dapat dipakai dalam ilmu psikologi, statistika, ilmu ekonomi, yaitu dalam bidang aktuaria dan lain-lain.
Dalam menghitung peluang, ada beberapa elemen yang harus kita ketahui sebelumnya.
Baca juga: Ingin Menang Undian lewat Lempar Koin Ini Rahasianya
Suatu proses disertai hasil dari suatu kejadian yang bergantung pada kesempatan. Jika percobaan dilakukan kembali, hasil yang diperoleh tidak selalu sama meskipun dilakukan dengan kondisi yang sama. Percobaan itu disebut dengan percobaan acak.
Ruang sampel adalah himpunan dari semua hasil yang mungkin terjadi dalam suatu percobaan.
Baca juga: Operasi Matematika dalam Bahasa Inggris dan Pengucapannya
Rumus Cepat Perkalian 2 Angka
Dirujuk dari buku Rumus Cepat Matematika untuk SD: Cara Mudah dan Cepat oleh Indah Hanaco, perkalian dua angka adalah salah satu tipe soal anak SD yang sering muncul. Jika mengerjakan dengan cara biasa, mungkin akan menyita waktu dan pikiran.
Selain cara konvensional (yang mungkin sulit untuk beberapa orang), ada cara alternatifnya, lho. Semisal, untuk perkalian 24 x 17, kamu bisa mengerjakannya dengan cara berikut:
Rumus Cepat Hitungan Kelipatan Kuadrat
Berikutnya, ada rumus untuk menghitung cepat hasil kuadrat suatu bilangan dengan pola berakhiran 5. Diambil dari buku Sukses Matematika SMP APiQ oleh Ir Agus Nggermanto. Sebagaimana telah diketahui,
15² = 22525² = 62535² = 122545² = ?
Polanya, dua angka di belakang hasilnya pastilah 25. Lalu, bagaimana cara menemukan angka di bagian depan? Caranya adalah mengalikan angka soal dengan 'kakaknya'.
Misal, untuk mendapat hasil angka depan 45², detikers perlu mengalikan 4 dengan 5 (karena 5 adalah 'kakak' dari 4). Jadi, hasilnya menjadi 2025. Hal yang sama juga berlaku untuk 6 (dikalikan 7) dan seterusnya. Bagaimana, mudah bukan?
Nah, itulah 5 rumus cepat matematika yang bisa detikers gunakan untuk mempermudah hitungan matematika sehari-hari. Semoga membantu!
Sifat-sifat peluang kejadian
1. Kisaran nilai peluang suatu kejadian adalah antara 0 sampai dengan 1 atau 0≤P(A)≤1. 2. P(A)=0, artinya peluang suatu kejadian yang tidak mungkin terjadi atau mustahil. 3. P(A)=1, artinya peluang suatu kejadian yang pasti terjadi.
Baca juga: UTBK SNBT 2024 Mitos dan Fakta, Sistem Penilaian, Kisi-Kisi Materi
n= total unsur keseluruhan r= banyaknya unsur yang akan diamati ! (faktorial)= perkalian semua bilangan asku yang kurang atau sama dengan n
Baca juga: UTBK SNBT 2024 Jadwal Penting, Pelaksanaan, Tata Tertib, Jenis Tes
n= total unsur keseluruhan r= banyaknya unsur yang akan diamati ! (faktorial)= perkalian semua bilangan asku yang kurang atau sama dengan n
Empat bola diambil secara acak dari boks yang berisi 15 buah bola. Karena salah penempatan, tiga bola kempis dan tidak bisa digunakan. Berapa peluang terambilnya empat bola yang tidak kempis?
Cari n(S) terlebih dahulu.
15C4 = 15!/(15-4)!4! 15C4 = 15x14x13x12x11!/11!4x3x2x1 15C4 = 1365
12C4 = 12!/(12-4)!4! 12C4 = 12x11x10x9x8!/8!4x3x2x1 12C4 = 495
Selanjutnya cari P(A).
P(A) = n(A)/n(S) P(A) = 495/1365 P(A) = 0,36
Semoga dapat dipahami. Selamat dan semangat belajar terus ya. (OL-14)
Sampai sekarang, matematika masih menjadi mata pelajaran menakutkan bagi banyak siswa. Bagaimana tidak, rumus-rumusnya terkadang sulit dipahami dan berjumlah banyak. Tenang, ada sejumlah rumus cepat yang bisa detikers pakai, lho!
Sesuai namanya, tujuan pengaplikasian rumus cepat adalah untuk bisa menyelesaikan suatu soal matematika dengan lebih cepat ketimbang pakai cara konvensional. Namun, perlu diingat bahwasanya terkadang, ada rumus cepat yang hanya bisa dipakai untuk soal tertentu.
Langsung saja, berikut ini 5 rumus cepat matematika yang bisa detikers praktikan. Pastikan untuk membaca penjelasan selengkapnya, ya!
SCROLL TO CONTINUE WITH CONTENT
Kumpulan Rumus Cepat Matematika dan Contoh Soalnya
Rumus Cepat Perkalian 3 Angka
Masih dikutip dari buku yang sama, ada juga rumus cepat untuk memecahkan perkalian 3 angka. Misalnya, 356 x 475, maka penyelesaian cepatnya adalah:
Letakkan semuanya secara berurutan sesuai tempatnya. Untuk memudahkan, bisa dilihat gambar berikut ini:
Kejadian/peristiwa peluang
Kejadian atau peristiwa peluang merupakan himpunan bagian dari ruang sampel. Biasanya dinotasikan dengan huruf kapital, seperti A,B,C.
P(A)= Peluang kejadian A n(A)= Banyak elemen A n(S)= Banyak elemen dari ruang sampel
Baca juga: Mengenal Sudut Istimewa Trigonometri dan Contoh Soal
Source by : Sugeng Supriyadi S.Kom, M.KomRead less
KOMPAS.com - Modus adalah anggota yang paling banyak muncul dalam suatu himpunan.
Dilansir dari buku Kumpulan Rumus Matematika SMA (2008) oleh Sri Lestari, modus pada data tunggal adalah data yang mempunyai frekuensi terbanyak.
Pada data dengan distribusi frekuensi berlaku rumus sebagai berikut:
Tb = tepi kelas bawah modusi = panjang intervala = frekuensi modusb = selisih frekuensi (modus) dengan kelas sesudahnya
Baca juga: Kumpulan Soal dan Jawaban Mencari Mean, Median, Modus pada Data Nilai Matematika
Dilansir dari buku Cerdas Belajar Matematika (2008) oleh Marthen Kanginan, untuk statistik data tunggal, modus adalah datum yang paling sering terjadi atau datum dengan frekuensi terbesar.
Untuk statistik data berkelompok, Anda dapat menaksir modus dari tabel distribusi frekuensi data berkelompok.
Modus dari data berkelompok dapat ditaksir dengan menggunakan rumus berikut:
Tb = tepi bawah kelas modus (kelas interval dengan frekuensi terbesar)Δf1 = selisih antara frekuensi kelas modus dan frekuensi tepat satu kelas sebelum kelas modusΔf2 = selisih antara frekuensi kelas modus dan frekuensi tepat satu kelas sesudah kelas modusp = panjang kelas interval pada kelas modus
Baca juga: Pengertian dan Rumus Mean, Median, Modus Pada Data Berkelompok
Tinggi badan siswa (cm) dalam suatu kelas sebagai berikut:
Jadi, modusnya adalah 150,32.
Baca juga: Cara Menentukan Modus
Tentukan modus dari tabel distribusi frekuensi data berkelompok berikut:
Untuk menghitung modus dari data berkelompok tersebut, Anda harus menentukan tepi kelas interval dari kelas modus (jika data ini belum diberikan dalam soal).
Pada tabel distribusi frekuensi yang diberikan, kelas modus terletak dalam batas kelas interval 156-160.
Dengan demikian, tepi kelas interval dari kelas modus adalah (156-0,5) sampai (160+0,5) = 155,5 sampai 160,5.
Dari interval tepi kelas modus ini diperoleh:
Baca juga: Menentukan Rata-rata, Median, dan Modus dari Data
Selanjutnya, lihat frekuensi-frekuensi kelas modus, tepat satu kelas sebelum kelas modus, dan tepat satu kelas sesudah kelas modus.
Pada tabel tersebut, tampak bahwa:
Δf1 = f-f1 = 13-12 = 1Δf2 = f-f2 = 13-10 = 3
Taksiran modus pasti berada dalam interval tepi kelas modus.
Dengan menggunakan rumus modus untuk data berkelompok, diperoleh:
Baca juga: Pengertian dan Contoh Soal dari Modus Ponens, Tollens, dan Silogisme
Kursus online calistung, Sains, hingga Matematika
Dokumen ini menjelaskan cara merangkum algoritma dengan 4 langkah: 1) input variabel, 2) output hasil, 3) metode penyelesaian masalah, 4) penugasan nilai variabel. Contoh algoritma menjumlah dan mengalikan dua bilangan digunakan untuk mendemonstrasikan langkah-langkah tersebut.
Academia.edu no longer supports Internet Explorer.
To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser.
Rumus Cepat Selisih Kuadrat
Perlu dicatat, rumus ini hanya berlaku jika satu bilangan kuadrat terbesar adalah hasil jumlah dari dua bilangan yang lain. Alias, sebagaimana dikutip dari buku Rumus Cepat Kuantitatif TPA, TIU & Matematika Dasar oleh Peris P Sitanggang, adalah a² - b² - c² = 2bc, jika a = b + c.
Misalnya, ada soal begini, hasil dari 75² - 35² - 40² =.... Berhubung 75 adalah hasil penjumlahan dari 35 + 40, maka rumus cepat ini bisa dipakai. Rumusnya adalah 2 x 30 x 45. Jadi, 75 = 35 + 40, maka 2 x 35 x 40 = 2800
Rumus Cepat Penjumlahan Waktu
Berdasar informasi dari buku Metode Menghitung Secepat Kilat! oleh NA Mastway, ada rumus cepat untuk menghitung penjumlahan waktu. Misalnya, untuk menjumlahkan 1 jam 35 menit dan 3 jam 55 menit, caranya menjadi:
Perlu dicatat, rumus ini hanya bisa dipakai apabila kedua waktunya ketika dijumlahkan bernilai di atas 60.



